sequence of collisions
This page explains how the 2D Rigid Body Physics Engine. deals with multiple simultaneous collisions. The summary points are:
The simulations discussed here use simplified rules to determine the result of a collision. A more exact simulation would model the deformation of the colliding bodies on a very small time scale. But that would require much more complex software and models, and would not run interactively in real-time.
The bottom line: although there isn't a single perfect solution, for most purposes the serial collision handling method works pretty well.
The book Physics-Based Animation by Erleben, Sporring, Henriksen, and Dohlmann discusses several approaches to handling collisions. In comparing two of the methods considered below, they write (on page 153):
We cannot really talk about one method being more correct or better than the other because it is possible to set up physical configurations of colliding rigid bodies where one of the methods computes the wanted motion and the other does not and vice versa.
The theory of rigid body collisions is described at Physics of Collision for Rigid Bodies in 2 Dimensions. That describes a single collision between two bodies at one collision point.
The key idea is that we can find a collision impulse which reverses the collision such that the final relative velocity between the bodies, vf , after the collision is some multiple of the initial relative velocity, vi .
| vf = −e vi | (1) |
The velocity here is the speed at which the gap distance between the objects is changing – their velocity relative to each other (not the absolute speed of the objects relative to the fixed background).
The elasticity e is a constant between 0 and 1 that indicates how "bouncy" the collision is, where e = 1 means perfectly elastic and e = 0 means completely inelastic.
When there are multiple simultaneous points of contact between two or more bodies then we have to modify the collision handling algorithm.
A typical case is when several bodies are in resting contact with each other and then another body crashes into one member of the group. Think of the initial "break" in a game of billiards where one ball collides into a large group of balls that are in resting contact with each other.
Another case is multiple simultaneous collisions. A typical case is a rectangular block colliding into a wall such that both corners are colliding. Another case is two bodies colliding from separate directions into a third body.
There are two ways to deal with multiple collisions
One method of handling multiple collisions is called the simultaneous collisions method. In this scheme, we predict the result at every point of collision or resting contact by using equation (1). We then find the appropriate collision impulse at each point of collision of contact such that the end result matches what equation (1) predicts.
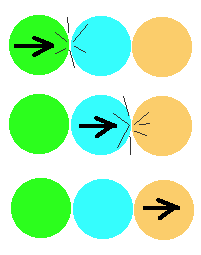
Consider a situation where there are two hockey pucks at rest and in contact with each other; and then a third puck comes from the left and strikes one of the pucks. (Imagine we are looking down onto an air hockey table).
We assume these hockey pucks are exactly lined up, elasticity is 1, and the pucks have the same mass. There are two points of collision, the collision on the left has a vi = −2 , the right collision has vi = 0 . By using equation (1) we get for the left collision vf = 2 and for the right collision vf = 0 . So we see the left puck bounce away to the left, and the pair of pucks move to the right remaining together.
This is the wrong behavior! If you play billiards, you know what should happen: the left and middle pucks should remain stationary, and the right-most puck should move away. Another example of the correct behavior is seen in the toy called a Newton's Cradle. It is a set of steel balls suspended from strings, such that they are resting against each other; when you pick up one of the balls at the end and let it hit the group, that ball stops and the ball at the other end flies away.
Consider just two hockey pucks, one stationary, and the other moving from the left. Suppose they have the same mass, are perfectly elastic ( e = 1 ), and the motion is aligned so they hit squarely. After they collide, the left puck should be stationary, and the right puck should move away. Because this is a single collision, equation (1) gives the correct result, with vf = −vi , and this is what we see in the Hockey Puck simulation. In the case of three hockey pucks, the same thing should happen: the velocity should transfer from the left puck to the right puck, with the impact transferred thru the middle puck.
Another way to see this: What if the two stationary pucks are not quite touching, but there is a small gap between them? Then, what happens is the "one hits one" collision happening twice, separated by a small gap of time and space. The Hockey Puck simulation below demonstrates this. Since you can make this gap as small as you want, it seems unreasonable that the behavior suddenly changes dramatically when the pucks are touching instead of separated by a tiny gap.

The serial collision handling method is also known by the terms propagating impulses or sequential collision handling. With the serial method, we imagine that each of the multiple collisions happens one at a time in sequence; we resolve each collision as a single collision, and then based on the resulting velocities there are subsequent collisions to resolve. All this happens instantaneously. It is rather like pretending that there are tiny gaps between the objects, and that they rebound against each other after the initial collision occurs.
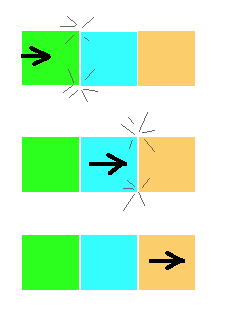
Consider the "one hits two" scenario, where one puck hits two motionless pucks that are in contact. With the simultaneous method, we used equation (1) to decide in advance what the final velocities would be at the two collision points (this was described above). The serial method goes thru a process of "collision resolving" where objects collide and rebound against each other, possibly many times, until there are no more collisions. This process of collision resolving takes no time, the idea being that because the objects are all in contact there is no distance for them to travel to bump into one another.
With the serial collision handling method, when elasticity e = 1 , the "one hits two" scenario goes like this: assume the left puck approaches the two stationary pucks with vi = −2
The result is that the left and middle pucks are stationary, and vf = 2 for the second collision. The simulation below runs this scenario with the serial collision method; it shows that the serial method correctly handles this case, in contrast to the simultaneous method.
Curious fact: With elasticity e = 1. we had only 2 collisions in the sequence. But with lower elasticity, such as e = 0.8 , you wind up with with an infinite series of smaller and smaller collisions as the middle puck collides back and forth between the left and right pucks.
The most obvious "problem" with serial collisions is when we have a square block instead of a round ball, and the two corners of the block hit an edge at the same moment. Here is a simulation of this; first with serial collision handling and then with simultaneous collision handling. Which do you think is more realistic?
Above is with serial collision handling. Below is the same situation with simultaneous collision handling.
Is this really a problem with serial collision handling? It would be very rare to have a collision happen in this mathematically precise way where both corners are colliding with the exact same speed. With a tiny change in the angle of the block, the simultaneous collision handling produces pretty much the same result as the serial handling as seen in the simulation below:
Earlier in discussing the "one hits two" scenario, we used the principle that "slight variations shouldn't radically change the solution". If we apply that principle here, then the serial collision handler actually looks like the better of the two.
Below is a situation where an object collides into two other objects at the same time. Again it is the case that the serial method gives a non-symmetric result, where the two collisions get different impulses because one is resolved before the other. If you choose "simultaneous" from the collision handling menu, you will see that the simultaneous solver gives a nice symmetric result. However if you put in a tiny starting angle (like 0.01) for the left block, then the result is similar to what the serial method produces.
Serial collision handling can result in an infinite loop of collisions. Here we show a couple such scenarios taken from Physics-Based Animation by Erleben, Sporring, Henriksen, and Dohlmann, section 6.2.1 "Nontermination of Sequential Collision Resolving" on page 154.
The first example shows two billiard balls wrapped in a frame. With perfect elasticity of 1.0, if an object strikes the frame, then the sequence of collisions "wraps around" and never terminates.
The simulation here is only able to cope with this situation because of some error handling code: when too many iterations are detected then the size of the acceptable "small velocity" is doubled; in the above case, this happens enough times that "small velocity" is greater than the actual original colliding velocity and we exit the loop. Note that energy is not conserved in this scenario which is another indication that this simulation is not correct.
The error-handling code only occurs with the "lastpass" collision methods: serial grouped lastpass or serial separate lastpass. If you choose instead serial group or serial separate and restart the simulation (click the rewind button and then the play button) then you will get an error alert when the collision occurs.
Another example from Erleben, et al, is of a heavy ball (mass 1000) striking a light ball (mass 1) which is at rest against a wall. With elasticity zero there is a sequence of collisions where the velocity changes by a factor of 1000/1001 with each collision, so the number of collisions is almost infinite.
Again the simulation is only able to cope with this scenario because of the error handling code that detects an infinite loop and then loosens the accuracy.
Here is a hybrid combination of the two approaches. It is like the serial method in resolving a sequence of individual collisions. But for each individual collision, it considers all the active collisions on that body. So we get a nice result for the "one hits two" case with square blocks (see the simulation below).
The first collision is solved simultaneously for both collisions at the corners between the left and middle blocks, so it gets a nice symmetric result: after the first collision the left block is stationary, and the middle block is moving to the right and starting to collide with the right block (see the picture at left). Next, the second collision is solved simultaneously for both corner collisions between the middle and right block, with the result that the middle block is stationary and the right block is moving.
Try selecting the other collision methods from the menu to see the difference; you should find that only the hybrid method gives the "correct" results.
This hybrid method decides which collisions to consider in each step as it resolves collisions serially. The criteria is something like this: Take the collision with the biggest velocity, which is between body A and body B; then add in any other significant collisions involving bodies A or B. Significant means any collision with a large velocity, so resting contacts are ignored.
This hybrid method also gives the nice symmetric result in the "one hits two separate" scenario shown below.
The hybrid model doesn't correctly handle cases where there are multiple collisions with unequal velocities, because it is based on using simultaneous collision handling for each individual "collision event". Below is an example where there are 2 simultaneous collisions, but at different velocities. What should happen is that the left and right pucks swap velocities, and the middle puck remains stationary.
The serial method gives the correct result for this case:
The correct result should be the same as if there were no middle puck; the impact forces should transfer through the middle puck (because the masses are all equal and elasticity is 1). Here is the situation with just 2 pucks, and any of the solvers gives the same result because only a single collision is involved.
In the myphysicslab 2D physics engine, joints are handled differently from normal collisions and contacts between rigid bodies. A joint is a permanent rigid connection between two bodies, or between a body and the (infinite mass) background. For example, in constructing a pendulum there are two joints made at the pivot point; one acts horizontally and the other acts vertically.
Here is an example collision scenario involving a pair of bodies that are jointed together.
The default collision handling method used in the myphysicslab simulations is called "serial grouped lastpass". It is a serial collision handling method, except that when joints are involved it does a simultaneous collision calculation involving all bodies connected by joints that are involved on either side of the collision. As with the hybrid method described above, there is still a sequence of collisions but the steps involving joints are calculated using the simultaneous method.
A different method of handling collisions involves placing tiny but very stiff springs at each collision point between objects. The simultaneous, serial and hybrid methods considered above all instantaneously resolve the collision with a set of impulses. In contrast, with spring based collision handling, the simulation continues to run during the collision. Because the springs involved are very stiff, the time steps taken during the collision must be very small.
The spring method gives the correct result for the "one hits one" situation, as seen in the simulation below. (This simulation is not a general rigid body simulation, but does show the results of using springs in simple linear collisions.)
But for the "one hits two" situation, the spring method gives an incorrect result. The left and middle block are moving after the collision, instead of remaining motionless as they should.
However, if you add a small gap between the two blocks then the behavior looks correct.