Double 2D Spring
Variables
This simulation shows two objects connected by springs and suspended from an anchor point. The objects are able to move in 2 dimensions and gravity operates. The anchor point is moveable.
You can drag either mass with your mouse. You can also drag the top anchor point. Click the "reset" button to put the masses in a resting equilibrium. Try changing parameters such as gravity, mass, spring stiffness, and friction (damping).
The math behind the simulation is shown below. Also available: source code, documentation and how to customize.
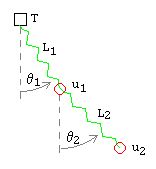
An immoveable (but draggable) anchor point has two spring2 and bobs hanging below and swinging in two dimensions. We regard the bobs as point masses. We label the upper spring and bob as number 1, the lower spring and bob as number 2.

Define the following variables:
Define some constants:
Note that for this simulation the vertical dimension increases downwards.
Here are the equations of motion. The derivation is similar to that given for the Single 2D Spring.
F1x = m1 a1x = −k1 S1 sin θ1 − b1 v1x + k2 S2 sin θ2
F1y = m1 a1y = −k1 S1 cos θ1 − b1 v1y + k2 S2 cos θ2 + m1 g
F2x = m2 a2x = −k2 S2 sin θ2 − b2 v2x
F2y = m2 a2y = −k2 S2 cos θ2 − b2 v2y + m2 g
The spring stretch Sn and angles θn are functions of the positions un of the bobs as follows:
L1 = √((u1x − Tx)2 + (u1y − Ty)2)
L2 = √((u2x − u1x)2 + (u2y − u1x)2)
S1 = L1 − R1
S2 = L2 − R2
cos θ1 = (u1y − Ty)/L1
sin θ1 = (u1x − Tx)/L1
cos θ2 = (u2y − u1y)/L2
sin θ2 = (u2x − u1x)/L2
To solve the equations of motion numerically, so that we can drive the simulation, we use the Runge Kutta method for solving sets of ordinary differential equations. We need to convert the four second order equations of motion to eight first order equations.
u1x' = v1x
u1y' = v1y
u2x' = v2x
u2y' = v2y
v1x' = −(k1/m1) S1 sin θ1 − (b1/m1) v1x + (k2/m1) S2 sin θ2
v1y' = −(k1/m1) S1 cos θ1 − (b1/m1) v1y + (k2/m1) S2 cos θ2 + g
v2x' = −(k2/m2) S2 sin θ2 − (b2/m2) v2x
v2y' = −(k2/m2) S2 cos θ2 − (b2/m2) v2y + g
We keep in mind that the spring stretch Sn and angles θn are functions of the position of the bob un as given previously.
This web page was first published April 2001.